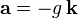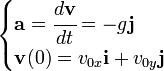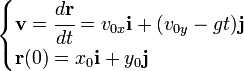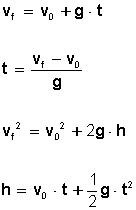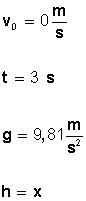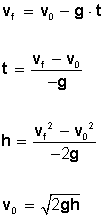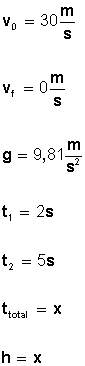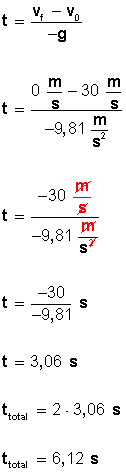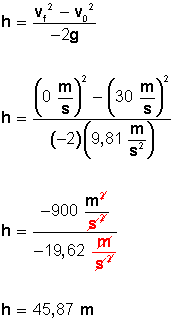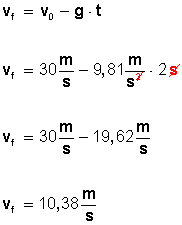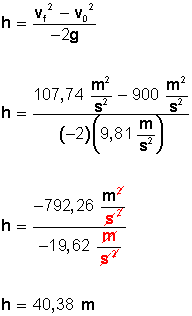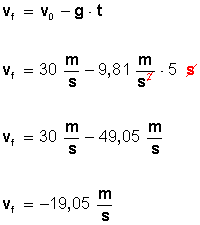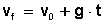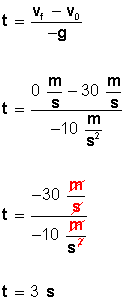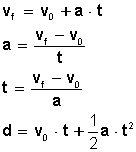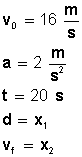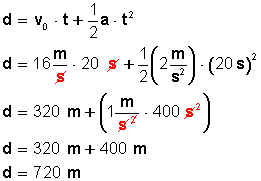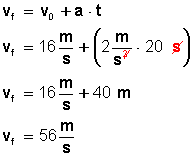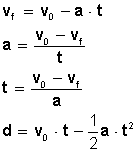LAS FUERZAS
El mundo está gobernado por una serie de fenómenos que suceden a nuestro alrededor sin que nos demos cuenta de ello o nos interesemos por observarlos en este caso observaremos a los fuerzas y como se relacionan con los elementos del medio, pero para estudiarlas primero tenemos que conocer algunos conceptos como: el peso que es el resultado de la interacción entre la tierra y todos los cuerpos que existen sobre ella y se define como el efecto de la gravedad sobre los cuerpos. Masa es la cantidad de materia que posé un cuerpo, ambos términos tienden a considerarse iguales pero ambos son magnitudes diferentes, el peso es una fuerza y se representa con una flecha hacia abajo, los cuerpos que poseen mayor cantidad de masa son más pesados.CLASES DE FUERZAS: Existen dos clases de fuerzas.
Las fuerzas a distancia: Son aquellas en las que los cuerpos que ejercen la fuerza no están en contacto directo, ejemplos de ellas son: la fuerza de gravedad, y las magnéticas.
Las fuerzas de contacto: Son aquellas cuando los cuerpos que la ejercen están en contacto como por ejemplo al empujar un baúl o rodamos un carrito de juguete sobre el suelo o también al dar un puntapié al balón de futbol.
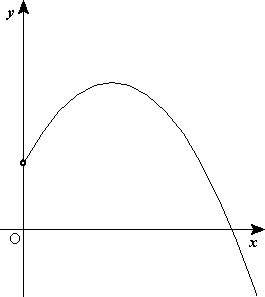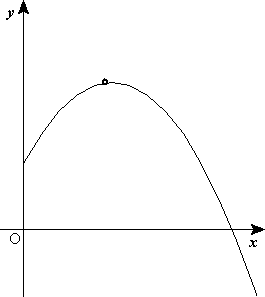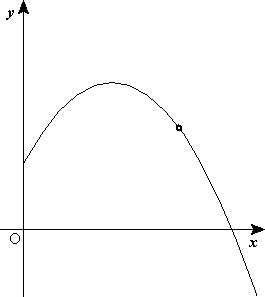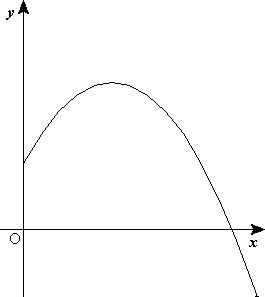
Descomposición de una fuerza: Una fuerza que actúa de forma oblicua sobre un cuerpo, como cuando se tira de un carrito de juguete con una cuerda con un ángulo de al menos 30° hacia la derecha por ejemplo, se le pueden calcular el valor de la componente vertical, hacia arriba Fy y la componente horizontal hacia la derecha Fx.

EFECTOS DE LOS FUERZAS: Las fuerzas de contacto son acciones ejercida entre los cuerpos y son capaces de: Producir deformaciones de los cuerpos, cambiando su forma.
Fig 1. Descomposición de una fuerza
Modificando el estado de movimiento o de equilibrio dinámico de un cuerpo, al cambiar su dirección.
Cambiando el estado de reposo o equilibrio estático, al ponerlo en movimiento.
La deformación de un cuerpo, originado por una fuerza depende de tres fenómenos: la intensidad de la fuerza, la superficie que se aplica y las características del cuerpo
FACTORES DE UNA FUERZA: Cuando se aplica una fuerza se pueden observar algunos elementos o factores del cuerpo afectado por la influencia de la fuerza ejercida por otro.
Punto de aplicación: Es la parte del cuerpo donde se está aplicando la fuerza.
Intensidad: Es el valor o la magnitud escalar de la fuerza ejercida, se usa el dinamómetro para medir el valor de esta.
Sentido: Señala hacia que sitio se ejerce la fuerza (arriba, abajo, derecha etc.)
Dirección: Nos indica la forma en que se ejerce la fuerza (horizontal, oblicua etc.)

Fig 2. Problema para practicar
Las fuerzas pueden medirse en una unidad llamada Newton y la fórmula utilizada para el cálculo es la siguiente:
F = m x a p = m x g
Donde: m es la masa: cuya unidad de medir es el kilogramo (Kg) en Sistema Internacional (SI), el gramo (g) en el sistema C.G.S y el slug en el sistema Inglés.
Donde: a es la aceleración: cuya unidad de medida es m/s2 en el SI, el cm/s2 en el C.G.S. y el pie/s2 en el sistema Inglés.
Donde: F es la fuerza: cuya unidad en el SI es el Newton, en el C.G.S la dina y el inglés es la libra-pie.
La aceleración de la gravedad en el SI es de 9.8 m/s2, en el C.G.S. es de 980 cm/s2, y el sistema Inglés es de 32 pies/s2.
Ejemplo:
Cuál es la fuerza resultante aplicada a una masa de 50 kg cuya aceleración es de 2 m/s2.
Datos: m = 50 Kg y a = 2 m/s2 incógnita = F
Solución. F = m x a
= 50Kg x 2 m/s2
F = 100 Kg-m = 100 Newton
LA FUERZA, EL MOVIMIENTO Y LA MASA:
Todos los cuerpos presentan una resistencia a modificar su estado en que se encuentra, ya sea en reposo o movimiento lo que se conoce como inercia: que es la tendencia de todos los cuerpos a conservar su estado de reposo o de movimiento.La intensidad de una fuerza aplicada a un cuerpo determina su movimiento. Al aplicar una fuerza a un cuerpo que ya está en movimiento, su velocidad cambia, lo que origina una aceleración, esta aceleración da un valor negativo cuando es una desaceleración. De esta explicación se deduce lo siguiente:
1. Si el cuerpo está en reposo comenzará a moverse si la fuerza aplicada es grande. Si el cuerpo está en movimiento con una velocidad determinada y constante, su velocidad cambiará si se aplica una fuerza grande. Así a = Vf - Vi/t
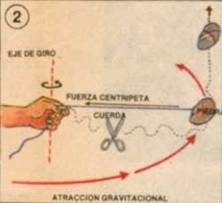
2. Cuanto mayor es la masa de un cuerpo en reposo mayor es la fuerza para ponerlo en movimiento. Y cuanto mayor es la masa de un cuerpo en movimiento mayor será la fuerza para aumentarle o disminuirle su velocidad.
LA FUERZA, El TRABAJO, LA POTENCIA Y LA ENERGIA: Y SUS UNIDADES DE MEDIDAS:
Al aplicarle una fuerza a cualquier cuerpo en reposo o movimiento produce cinco fenómenos: movimiento, desplazamiento, trabajo, energía y la potencia. El desplazamiento se puede medir en metros (m), centímetros (cm), o pies. El trabajo se expresa en Newton-metro (N.m), o Joule (J) o en dinas o libra-pie. La potencia se mide en N.m/s o J/s = Watts o vatios (W) o caballo de fuerza (HP). La energía cinética se expresa en Kgm o Julio (J), cada una de las unidades dependerá del sistema de medida o las unidades de medidas utilizadas. Veamos algunos ejemplos.
http://www.blogger.com/goog_99661048
EL TRABAJO:
Ejemplo: Para desplazar un objeto hasta una distancia de 4 metros es necesario aplicar una fuerza constante de 25 N. ¿Cuál será el valor del trabajo desarrollado?Trabajo: W = F x d
W = 25 N x 4 m o W = 25 N x 4 m
W = 100 N.m o W = 100 J
LA POTENCIA:
La potencia: Es la relación que existe entre el trabajo desarrollado y el tiempo empleado para ejercerlo. Si obtenemos los datos del problema anterior. ¿Cuál sería la potencia si tardó 5 segundos en realizar el trabajo?Potencia: P = F x d/t o P = W/t
P = 25Nx4m/5seg o P = 100J/5seg
P = 20 watts P = 20 watts
735 watts = a un HP, si queremos cambiar la potencia a HP sería: 20W/735x1HP= 0.027HP
http://educacion.practicopedia.com/como-actuan-las-fuerzas-2051
http://www.videosurf.com/video/teorema-del-trabajo-y-la-energ-a-cin-tica-108713573
ENERGÍA:
Energía cinética: La que posee un cuerpo debido a su movimiento, es la capacidad de hacer trabajo y es directamente proporcional tanto a la masa como a la velocidad.http://es.wikipedia.org/wiki/Potencia_(f%C3%ADsica)
Energía cinética Ec = ½ x m x v2
Ejemplo: ¿De cuanto es la energía cinética de un auto cuya masa es 2000 kilogramos viajando a una velocidad de 20 m/seg?
Ec = ½ x m x v2
Ec = ½ x 2000 Kg x (20 m/s)2
Ec = ½ x 2000 Kg x 400 m2/s2
Ec = 400,000 Kgm
http://es.wikipedia.org/wiki/Energ%C3%ADa_cin%C3%A9tica#Energ.C3.ADa_cin.C3.A9tica_en_mec.C3.A1nica_newtoniana
Energía potencial: Es la que posee un cuerpo debido a la posición (altura).
Energía potencial: Ep = m x g x h o Ep = p x h
Ejemplo: Cuál es la energía potencial de un cuerpo cuya masa es 5 kilogramos que se localiza a una altura de 5 metros.
EP = m . g . h o Ep = p . h
Ep = 5Kg x 9.8m/s2 x 5 m o Ep = 49 Kg x 5 m
Ep = 245 Kgm o Ep = 245 Kgm
http://es.wikipedia.org/wiki/Energ%C3%ADa_potencial#Energ.C3.ADa_potencial_gravitatoria
Energía mecánica:
La energí a mecánica es el resultado de la energía cinética y la energía potencial, por lo tanto la energía mecánica es la suma de ambas energía así. Em=Ec+Ep, Según la fórmula:
1. Si la energía cinética aumenta la energía potencial disminuye.
2. Si la energía potencial aumenta la energía cinética disminuye.
Esto se debe al principio de conservación de la energía que dice: La energía no se crea ni se destruye solamente se transforma.
Información según: El Profesor Cirilo Didier Navarro



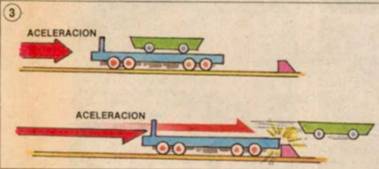
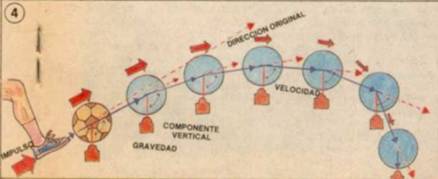





 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad.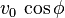 que se denomina componente horizontal de la velocidad inicial.En lo sucesivo
que se denomina componente horizontal de la velocidad inicial.En lo sucesivo 
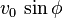 que se denomina componente vertical de la velocidad inicial.En lo sucesivo
que se denomina componente vertical de la velocidad inicial.En lo sucesivo 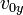
 : [ecu. 1]
: [ecu. 1]